Satellites troyens de Jupiter
Troyens (Grec) sur L4 - 249 astéroides
588 Achille – 100 Km (1906)
624 Hector – 140 Km (1907)
659 Nestor – 70 Km (1908)
911 Agamemnon – 170 Km (1919)
1143 Odyssée – 115 Km (1930)
…
Troyens (Troyens) sur L5 - 167 astéroïdes
617 Patrocle – 110 Km (1906)
884 Priam – 75 Km (1917)
…

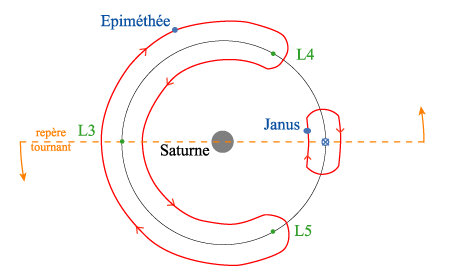
Satellites Troyen du système de Saturne :
Epiméthée : Sur l’orbite L4,L3,L5 en fer à cheval de Janus
Télesto & Calypso : Aux points L4 & L5 de Téthys
Hélène : Troyen L4 de Dioné
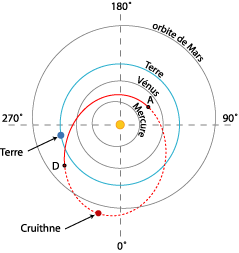
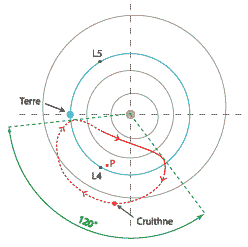
Troyen de la Terre
Astéroïde 3753 Cruithne
De la famille Aten - 4 Kms - découvert en 1986
Sur l’orbite L4 en fer à cheval
Compagnon de la Terre en résonance 1:1
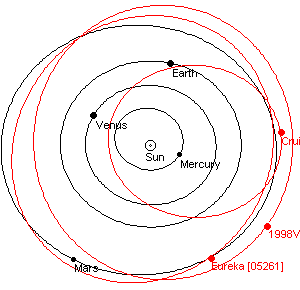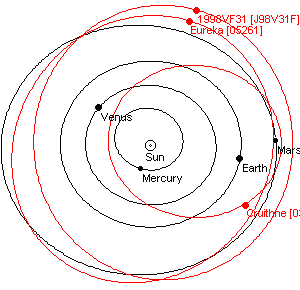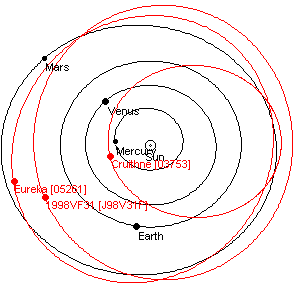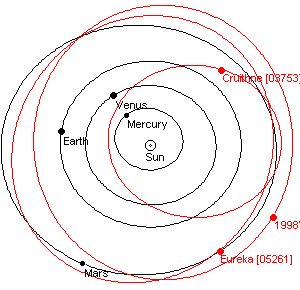
Troyen de Mars
Astéroïdes 5261 Eurêka & 1998 VF 31
Sur l’orbite en fer à cheval L5 (suit Mars)
Attention, tourne dans le sens des aiguilles d'une montre !?

Points de Lagrange
Prenons l'exemple du système Terre - Soleil, où la Terre a une orbite quasi circulaire autour du Soleil.
Un 3ème corps, de masse négligeable, se maintient en équilibre sur des points particuliers où toutes les forces se compensent :
L1, L2, L3 sont des points d’équilibre instables
L4, L5 sont des points d’équilibre stables. Ce sont des cas particuliers d’une résonance orbitale 1:1
Les satellites en L4 et L5 sont appelés 'troyens'
Travaux publiés en 1788 par le mathématicien d'origine italienne Joseph-Louis Comte de Lagrange.
Cas du système Terre-Soleil
Sphère d’influence (Sphère de Hill)
En présence de 3 corps (Planète, Satellite, Soleil), un satellite ne peut pas exister au delà de la sphère d’influence de la Planète : Il serait éjecté de l’orbite planétaire où il se trouve, par le Soleil pour se retrouver sur une orbite héliocentrique.
'La Lune serait arrachée à la Terre par le Soleil si elle se trouvait à plus de 1 700 000 Km de la Terre (4 fois la distance actuelle)'. A.Brahic
Un gros satellite ne peut donc exister qu’à une distance de la planète comprise entre :
LR : Limite de Roche, la limite inférieure
Ri : Rayon de la sphère d’influence , la limite supérieure
Le rayon de la sphère d'influence d'une planète est fonction de la masse de la planète, mais surtout de l'éloignement du Soleil.
-> Neptune a une sphère d'influence plus grande que Jupiter bien que sa masse soit plus faible.
D'après l'article de Wikipédia sur la sphère de Hill
Influences gravitationnelles
dans le système solaire
Références documentaires
Planètes et Satellites, 5 leçons d'astronomie - André Brahic - Vuibert
Aux confins du système solaire - A. Doressoundiram, E.Lellouch - Belin - Pour la Science
Mouvement rétrograde des satellites de Jupiter
On observe une répartition particulière des satellites de Jupiter :
Une zone d’exclusion : Aucun satellite entre 12 et 18 millions de kilomètres
Au delà de 18 millions de km : Tous les satellites ont une rotation rétrograde
La zone d’exclusion, sans satellites , s’explique par les perturbations gravitationnelles du soleil :
La zone d’exclusion est due au mécanisme de Kozai.
A cause de l’éloignement du satellite par rapport à la planète, les perturbations gravitationnelles du Soleil sont importantes.
Cela entraîne une oscillation couplée de l’excentricité de l’orbite du satellite et de son inclinaison par rapport au plan de l’écliptique .
La théorie du chaos est l’hypothèse actuelle pour expliquer les orbites rétrogrades :
Les satellites rétrogrades sont souvent trop loin pour avoir été formé dans la sous nébuleuse proto planétaire primitive :
La capture ou les collisions d’astéroïdes ou de comètes semble l’hypothèse la plus probable.
Les orbites rétrogrades qui sont à la limite de la zone d’influence de la planète sont plus stables que les orbites progrades, plus chaotiques.
Ce mécanisme tend donc à produire plus d’orbites rétrogrades.

Satellites bergers de l'anneau Epsilon d'Uranus
Confinement gravitationnel dans les anneaux - Satellites bergers
La combinaison de la gravitation, de résonances et de collisions provoque un effet de répulsion des corps.
Anneau F de Saturne confiné par 2 satellites “gardiens” : Pandore et Prométhée
L'anneau F orbite à 140 120 km du centre de Saturne
Anneau Epsilon d’Uranus confiné par 2 satellites “gardiens” : Cordélia et Ophélia
Cordélia en résonance 25:24 avec le bord interne de l'anneau
Ophélia en résonance 13:14 avec le bord externe de l'anneau

Résonances dans les anneaux de Saturne
Bord externe de B en résonance 2:1 avec Mimas
Bord externe de A en résonance 7:6 avec Janus et Epiméthée
Résonance des satellites de Jupiter
Résonances de “Laplace” . Mr le Marquis a étudié ces relations de commensurabilité 4:2:1
Io : 1,77 Jours
Europe : 3,55 Jours Résonance 2:1 avec Io
Ganymède : 7,16 Jours Résonance 2:1 avec Europe
Résonances de révolution des planètes :
Vénus :
Vénus est en résonance 13:8 avec la Terre. En 8 ans, Vénus effectue 13 révolutions autour du Soleil :
224.7 j * 13 = 365.25 j * 8 (Environ 2922 jours).
En outre, Vénus effectue 5 révolutions synodiques en 8 ans :
583.9 j * 5 = 365.25 j *8 (Explique l'origine du Pentagramme esotérique lié à Vénus).
Vénus effectue 2.6 révolutions quand la Terre en effectue 1.6 : Voir le gif
Planètes externes :
Jupiter : 11,86 ans
Saturne : 29,46 ans Résonance 5 : 2 avec Jupiter
Uranus : 84,01 ans Résonance 3 : 1 avec Saturne
Neptune : 164,79 ans Résonance 2 : 1 avec Uranus
Pluton : 248,43 ans Résonance 3 : 2 avec Neptune
Pluton et Neptune n’entreront jamais en collision grâce à cette résonance
Résonances orbitales :
Amplification des interactions gravitationnelles entre planètes ou entre planètes et satellites lorsque les périodes de révolution de leurs orbites respectives adoptent des rapports entiers , notés m : n.
Les résonances les plus fortes sont celles qui correspondent à des rapports où m = n+1 (2:1, 4:3 …)
Résonance des satellites de Saturne
Mimas : 0,94 Jours
Encélade : 1,37 Jours
Téthys : 1,89 Jours Résonance 2:1 avec Mimas
Dioné : 2,74 Jours Résonance 2:1 avec Encelade
Titan : 15,90 Jours
Hypérion : 21,30 Jours Résonance 4:3 avec Titan
Résonance Titan - Hypérion :
Titan s’éloigne de Saturne par effet de marée, comme la Lune avec la Terre.
Par résonance , Titan entraine Hypérion, beaucoup plus petit que lui, dans son éloignement de Saturne.
Sans cette résonance , Hypérion serait probablement entré un jour en collision avec Titan.
=> La résonance a un rôle de “préservation“ des orbites

Résonances orbitales des planètes et satellites
Ceinture principale d’astéroïdes - Lacunes et résonances
Deux phénomènes observés dans la ceinture d'astéroïdes
Résonances avec Jupiter (concentration d'astéroïdes)
279 Thule en résonance 4:3
Famille de Hilda en résonance 3:2
Lacunes découvertes en 1866 par Daniel Kirkwood (zones sans astéroïdes)
Lacunes aux résonances 4:1, 7:2, 3:1, 5:2, 7:3, et 2:1
J. Wisdom a expliqué, par la théorie du chaos, la division en résonance 3:1 avec Jupiter :
1. Astéroide sur une orbite stable, en résonance , pendant 1 million d’années …
2. Faible perturbation => brusque augmentation de l’excentricité de l’orbite
3. L’orbite de l’astéroide se rapproche de celle de Mars ou de la Terre
4. Pertubation de l’orbite et éjection vers une nouvelle orbite
-> Ce processus vide la résonance 3:1 qui devient une division (“lacune”)
Ceinture de Kuiper et Objets Transneptuniens (TNO) - Résonances
Une vue d'ensemble des Objets Transneptuniens (Crédit Wiki) :
Pluton, Hauméa, Makémaké, Eris ont été classées 'Planètes naines'
En Abscisse : UA (10 à 70) / Périodes de Révolution en années (100 à 600) / Résonances
En Ordonnée : Inclinaison des orbites sur l'écliptique, en degrés


Résonances des objets de la ceinture de Kuiper.
Crédit : 'Aux confins du système solaire' - Belin Pour la Science - A.Doressoundiram, E.Lellouch
La 'falaise de Kuiper' :
Les objets de la ceinture de Kuiper se répartissent principalement à des distances autour de 40 UA et entre 42 et 48 UA (Crédit Wiki)
Au delà de 48 UA, distance à laquelle les objets sont en résonance 2:1, on observe beaucoup moins d'objets, une troncature du disque comme s'il s' agissait de la limite externe de la ceinture de Kuiper.
Les plutinos en résonance 3:4 avec Neptune :
Orcus, Ixion ...
Pluton & Charon en résonance 2:3
(vu plus haut au premier paragraphe)
Les Cubewanos (du premier objet découvert 1992 QB1 ) en résonance 3:5 et 4:7 :
Makémaké, Hauméa, 1992 QB1, Varuna, Quaoar, .....
Les Twotinos en résonance 1:2 avec Neptune (d'où leur nom)

On observe, dans les objets transneptuniens, de nombreuses résonances orbitales avec Neptune :


Crédit : 'Aux confins du système solaire' - Belin Pour la Science - Alain Doressoundiram
Il manque de la masse !
La masse actuelle de la ceinture de Kuiper est très faible, On pense qu'elle doit être comprise entre 0.01 et 0.1 masse terrestre., ce qui est insuffisant pour que des objets de la taille de Pluton ou Eris aient pu se former. Il en faudrait 100 à 1000 fois plus !
Si la plupart des objets transneptuniens sont stables, quel mécanisme a pu retirer au moins 99% de la masse initiale présente dans les régions transneptuniennes ?
(D'après 'Aux confins du système solaire' (Belin - Pour la Science)