Calendrier lunaire

La face 'calendrier lunaire' de l'instrument permet de trouver l'âge de la Lune pour une date donnée.
a) A partir de l'année considérée, on trouve :
le Nombre d'or (pour information)
et l'Epacte, l'age de la Lune au 1er janvier avec le cercle au centre de l'instrument.
b) Lorsque les calendriers lunaire (couronne extérieure) et solaire (couronne intérieure) sont correctement alignés avec l'épacte de l'année considérée, on vient lire l'âge de la Lune (graduations extérieures de la couronne extérieure) ou la phase de la Lune (graduations intérieures de la couronne extérieure) pour une date quelconque de l'année (graduation extérieure de la couronne intérieure)
C) Entre le calendrier solaire et le cercle de calcul de l'épacte au centre, les signes zodiacaux astrologiques (dates fixes par rapport au calendrier grégorien)
Le calcul de l'épacte de l'instrument est utilisable entre les années 2008, première année de référence pratique, et 2199, pour éviter le décalage séculaire du cycle métonique.
Exemple 1
Age de la Lune le 7 avril 2014 - PQ (Premier quartier) :
2014 = 2008 + 6 ans : L'épacte = 29, Le Nombre d'Or = 1
On place le curseur du calendrier solaire (1er janvier) sur la graduation 29 (épacte)
On lit en face du 7 avril : Age de la Lune = 7 jours. Les graduations étant très raprochées, on peut estimer l'incertitude de la lecture de l'âge de la Lune d'une graduation (1 jour). Il manque peut être une alidade pour bien matérialiser le rayon de l'instrument.
Si l'on vérifie l'âge de la Lune avec des éphémérides :
Le 7 avril à 0h TU : 7j 5h 15mn
Le 7 avril à 12h TU : 7j 17h 15mn
Le 8 avril à 0h TU : 8j 5h 15 mn
Exemple 2
Age de la Lune le 15 avril 2014 - PL (Pleine Lune, Syzygie) :
On lit en face du 15 avril : Age de la Lune = 15 jours.
Si l'on vérifie l'âge de la Lune avec des éphémérides :
Le 15 avril à 0h TU : 15j 5h 15mn
Le 15 avril à 12h TU : 15j 17h 15mn
Le 16 avril à 0h TU : 16j 5h 15 mn
Calculateur de marée (heure solaire de la pleine mer)

Exemple 1
Heure solaire de pleine mer à Brest le 7 avril 2014 - PQ (Premier Quartier) :
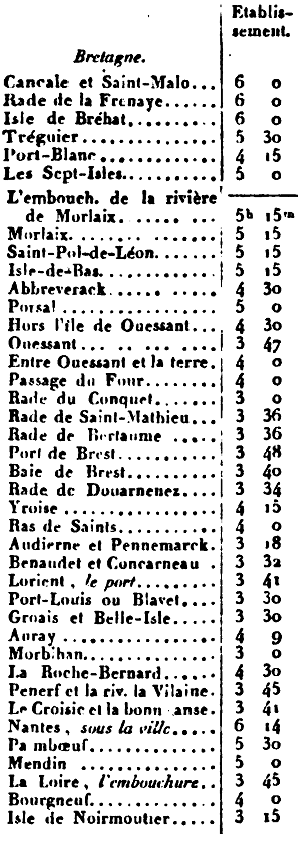
Etablissement du Port de Brest : 3h 48 mn (Charles Guepratte 1848)
Age de la Lune lue précédemment sur la face du calendrier lunaire de l'instrument : 7 jours
Heure solaire de la pleine mer par le calcul : 12h + 3h 48mn + 50mn * 7 (jours) = 21h 38mn
Heure solaire lue sur le cadran de l'instrument (7 j) : 21h 25mn
Heure légale à partir de l'heure solaire de Brest :
Equation du temps pour le 7 avril (voir table plus haut) : +2mn (+2mn 16s. le 07/04/2014 à 0h avec Coelix Apex)
Longitude de Brest : -4° 30' => Correction de l'heure solaire moyenne (1° = 4mn) : + 18mn
Fuseau horaire : +1 h, Heure d'été : +1 h
Il faut donc ajouter 2h 20mn à l'heure solaire vraie pour obtenir l'heure légale, ce 7 avril à Brest.
L'heure légale de pleine mer : 21h25 (heure solaire lue) + 2h20 (corrections) = 23h 45mn
Heures des marées à Brest le 7 avril 2014 (Heures TU+2) : Voir les Prédictions en ligne du SHOM
05h09 BM
11h07 PM 38
17h32 BM
23h39 PM 34
Je trouve donc un écart sur l'heure de la pleine mer négligeable de +6 mn ... avec une incertitude de 1 graduation (50 mn)
La face 'calculateur de marée' permet de trouver l'heure solaire de la pleine mer d'un port donné connaissant :
1) L'établissement du port (le décalage moyen de l'heure de la pleine mer sur le passage de la Lune au méridien, pour le port considéré)
2) L'âge de la Lune pour une date donnée, trouvé sur l'autre face de l'instrument.
La couronne extérieure graduée de I à XXIIII représente l'heure solaire de la marée.
La couronne intérieure est graduée en 'âge de la Lune' de 0 à 29.5 jours. Chaque jour de lunaison ajoute un décalage supplémentaire de 50mn. La précision de l'âge de la Lune sur cette face est bien plus grande que sur l'autre face.
Au centre les 32 rumbs, les 32 quarts de vents antiques. Voir le paragraphe dédié, plus loin.
Exemple 2
Heure solaire de pleine mer à Brest le 15 avril 2014 - PL (pleine Lune) :
Etablissement du Port de Brest : 3h 48 mn
Age de la Lune lue précédemment sur la face du calendrier lunaire de l'instrument : 15 jours
Heure solaire de la pleine mer par le calcul : 12h + 3h 48mn + 50mn * 15 (jours) = 04h 18mn
Heure solaire lue sur le cadran de l'instrument : 04h 00mn (Le lendemain matin ?)
Heure légale à partir de l'heure solaire de Brest :
Equation du temps pour le 15 avril (voir table plus haut) : 0 mn (+0 mn 10s. le 15/04/2014 à 0h avec Coelix Apex)
Longitude de Brest : -4° 30' => Correction de l'heure solaire moyenne (1° = 4mn) : + 18mn
Fuseau horaire : +1 h, Heure d'été : +1 h
Il faut donc ajouter 2h 18mn à l'heure solaire vraie pour obtenir l'heure légale, le 15 avril à Brest.
L'heure légale de pleine mer : 04h 00mn (heure solaire lue) + 2h 18mn (corrections) = 06h 18mn
Heures des marées à Brest le 15 avril 2014 (SHOM) : Heures TU+2
05h54 PM 91
12h16 BM
18h12 PM 93
00h31 BM
06h30 PM 95 (le 16/04)
Je trouve donc un écart de -12mn en considérant que l'heure de la pleine mer calculée est bien celle du lendemain matin 16 avril.
Pour lire l'heure solaire de la marée, on procède ainsi :
a) Curseur de la couronne intérieure sur 12h (XXIIII)
b) Ajout de l'établissement du port
c) Ajout de l'age de la Lune.
Les membres du Club d'Astronomie du Trégor m'ont offert un magnifique instrument inspiré d'instruments anciens du XVIe et XVIIe siècles (H.Cole and the English School ...) tels que les volvelles de Denoville, la Volvelle des ports par exemple.
Cet instrument permet de calculer l'heure solaire vraie de la pleine mer pour une date donnée et un lieu donné connaissant 'l'établissement du port'. Les calculs sont basés sur l'âge de la Lune et donc sur le calendrier lunaire.
Voir les photos de cet événement sur la page relatant mes sorties avec le Club d'Astronomie du Trégor
Cette page présente l'instrument en 4 chapitres :
Glossaire
Quelques notions utiles à rappeler pour bien comprendre le fonctionnement de cet instrument
Heure légale, heure UTC, heure solaire vraie et heure solaire moyenne
Pour obtenir l'heure légale à partir de l'heure solaire vraie, il faut appliquer les corrections suivantes :
a) L'équation du temps :
Le mouvement apparent du Soleil n'est pas uniforme tout au long de l'année. Le Soleil ne se déplace pas sur l'écliptique à vitesse constante.
Il s'ensuit que la durée du jour solaire varie d'une quarantaine de secondes suivant la date. Le passage du Soleil au méridien peut donc être en avance ou en retard, jusqu'à un quart d'heure, par rapport au temps moyen de nos horloges.
Voir plus loin ci dessous une explication plus détaillée sur 'L'équation du temps'
b) La longitude du lieu par rapport au méridien de Greenwich
L'heure légale est la même sur tout le fuseau horaire, cependant l'heure solaire varie continûement d'Est en Ouest. A l'Ouest du méridien de Greenwich il faut rajouter le temps correspondant au décalage horaire vrai de la longitude du lieu, à l'Est il faut retirer ce décalage de temps.
1 heure (un fuseau horaire) représente 15° de longitude, 4mn : 1° de longitude et 4 s. : 1' de longitude.
c) L'heure du fuseau horaire (heure d'hiver)
Pour la France métropolitaine, l'heure d'hiver = UTC + 1h .
C'est en fait l'heure du fuseau horaire de l'Europe Centrale car le méridien de Paris n'est situé qu'à 2° 20' 13,82" à l'est de celui de Greenwich.
d) L'heure d'été (Daylight saving in English)
Pour la France métropolitaine, l'heure d'été = UTC + 2h
Le temps solaire moyen
Le temps solaire moyen est le temps solaire vrai corrigé de l'équation du temps.
Le Temps Universel Coordonné (UTC) :
C'est la référence de temps utilisée pour le temps civil sur Terre.
Le temps UTC est égal au Temps Universel (TU) corrigé de secondes intercalaires ajoutées (ou pas) à dates fixes en milieu et fin d'année pour suivre le Temps Atomique International (TAI) basé sur la définition de la seconde.
Le Temps Universel (TU) remplace le Temps Moyen de Greenwich (GMT). Ce temps suit la rotation de la Terre.
Le temps TAI est actuellement en avance de 35s. sur le temps UTC.
Année tropique et Calendrier Grégorien
L'année tropique est l'année du retour des saisons. Elle est la base des calendriers solaires.
L'année tropique est définie comme l'intervalle de temps dans lequel la longitude moyenne du Soleil sur son orbite apparente, l'écliptique, croît de 360°.
La durée de l'année tropique en l'an 2000 était de 365,24219 soit soit 365 j 5 h 48 min 45,26 s
Le calendrier Grégorien utilisé aujourd'hui suit l'année tropique. Il corrige les dérives séculaires de l'ancien calendrier Julien par des ajustements particuliers sur les années bissextiles.
Equation du temps
L'équation du temps est en fait la résultante de deux effets :
L'équation du centre due à l'excentricité de l'orbite terrestre (la trajectoire de la Terre est elliptique et non circulaire)
La réduction à l'équateur due à l'obliquité de l'écliptique (la Terre ne tourne pas dans son plan équatorial autour du Soleil) puisque l'on mesure le passage du Soleil au méridien du lieu par rapport au plan équatorial terrestre dans lequel il faut donc le ramener.
L'excentricité de l'orbite terrestre et l'obliquité de l'écliptique varie lentement au cours des siècles.
Etablissement du Port
La théorie de Newton prévoit que l'heure la pleine mer correspond au passage de la Lune au méridien. La réalité est différente.
L'établissement du port est le retard de la pleine mer sur le passage de la Lune au méridien, pour un lieu donné. Il est défini pour une conjonction avec une distance Terre Lune moyenne, et une déclinaison nulle du Soleil et de la Lune. A cause de la variation de ces paramètres (Vives eaux de syzygie ou mortes eaux de quadrature ...) l'établissement du port connait des variations.
Les calculs réalisés avec l'instrument présenté ici ne peut donc être qu'une estimation.
Les baies fermées ont un régime hydrographique particulier. Dans le Golfe du Morbihan par exemple, le marnage diminue en vives eaux et l'onde de marée met 1h30 (mortes eaux) à 2h (vives eaux) pour parcourir tout le golfe, aussi bien à marée montante qu'à marée descendante. Il n'y a pas de dyssimétrie flagrante entre flot et jusant.
La dyssimétrie flot-jusant est peu importante en Atlantique. En manche, par contre, la dyssimétrie augmente vers l'est. Un exemple pour St Malo le 21/03/2015 : Le flot est de 5h17mn et le jusant de 7h05.
D'après 'Tout savoir sur les marées' - Odile Guérin.
Lunaison et période de révolution synodique de la Lune
La lunaison est l'intervalle de temps entre 2 nouvelles lunes, soit une durée moyenne de 29 jours 12 heures 44 minutes et 2,9 secondes. La durée du mois synodique est de 29.53 jours
La durée des lunaisons varie au cours d'une année (de l'ordre de ±6 h) et même d'une année à l'autre
La période synodique correspond à la lunaison, où l'on retrouve la même configuration Soleil-Terre-Lune.
L'alignement de 3 corps en opposition ou en conjonction, notamment l'alignement Soleil-Terre-Lune à la nouvelle Lune ou la pleine Lune s'appelle une Syzygie.
La période sidérale (jour sidéral) de la Lune est de 27.32 jours (Temps pour pointer la même direction du ciel)
Année lunaire
La durée d'une année lunaire de 12 mois lunaires (lunaisons) est de 354.36 jours.
Une année solaire faisant 365.24 jours, il y a un écart de près de onze jours entre les 2 années (10.88 jours), d'où le décalage des phases de la Lune d'une année sur l'autre dans notre calendrier solaire.
Cycle de Méton
Le cycle métonique est un commun multiple approximatif des périodes orbitales de la Terre et de la Lune.
235 lunaisons = 19 années tropiques à 1h 27mn 33s près. La différence atteint 1 jour au bout de de 312.5 ans.
Tous les 19 ans la Lune
Nombre d'or
Le rang d'une année dans le cycle métonique s'appelle le 'Nombre d'or'
Le nombre d'or = (l'année modulo 19) +1
Age de la Lune
L'âge de la Lune est le nombre de jours écoulés depuis la nouvelle Lune.
Voir le site de l'IMCCE sur les phases de la Lune
Epacte
C'est l'age de la Lune au 1er Janvier de l'année.
Permet de connaître, pour l'année considérée, les dates des phases de la Lune.
L'épacte sert dans le Comput chrétien à calculer la date de Pâques
Voir le site de l'IMCCE sur l'équation du temps
Voir également le site de Jean-Paul Cornec, membre de la commission des Cadrans Solaires de la SAF
Courbes créées avec le logiciel Shadows
Ephémérides créées avec le logiciel 'Coelix Apex'
Table extraite de l'ouvrage 'Problèmes d'astronomie nautique et de navigation' de C.Guepratte - 1839
Rose des vents de l'antiquité
L'instrument présente sur la face 'calculateur de marée' une rose des vents antiques, grecs et romains tels qu'ils étaient représentés dans les volvelles (voir l'introduction)
Les documents trouvés sur le web (Mappemondes - BNF , Mémoire sur la collection des grands et des petits voyages dont un extrait est présenté ci dessous ...) ne sont pas toujours d'accord entre eux la direction des vents. Il existe aussi une grande diversité des noms et de l'orthographe des noms de vents.
Je présente plus loin la version de la rose des vents de l'instrument.
Un Rumb (Rhumb) ou 1/4 de vent est un secteur de 1/32e de la rose des vents couvrant un angle de 11°25'. Les Rumbs sont numérotés de 1 à 32 dans le sens horaire en partant du nord.
Les anciens prêtaient aux vents de bonnes ou mauvaises vertues. Le vent d'ouest (Favonius ou Zephyr en Grec) est favorable; le vent du Sud (Auster, Notos) est sec; le vent du Nord (Septentrion, Aquilon) est glacial ...

Les 32 Rhumbs (1/4 de vents) . Noms de vents de l'antiquité grecque et romaine

Ci dessous, la transcription de la rose des vents de l'instrument.
Les vents d'ouest sont gravés sur la droite de l'instrument (Explication ?)
Trois jours après la pleine lune, la mer fait son plus grand saut




